spezielle Relativitätstheorie / Minkowski-Raum                    zurück Rundschreiben an Professoren
      6.2.05
Bei der Achse in nebenstehendem Text handelt es sich vermutlich um eine Ebene, daher versuche ich mir die Drehung eines vierdimensionalen Raumes um eine 2dimensionale Achse vorzustellen, sowie daraus die Definition eines komplexen Winkels zu recherchieren. (2.Arbeitshypothese, A2: Eine (wechselnde oder konstante) 1dim-Achse plus komplexer Winkel genügt für eine exakt definierte Rotation.)
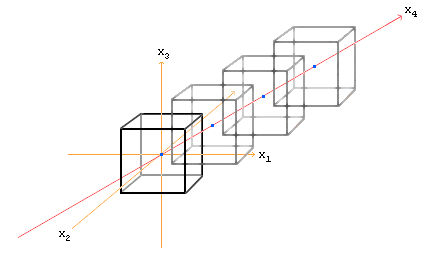
"Achse durch Nullpunkt orthogonal zur x1/x4 -Ebene"  bedeutet, bei der Bewegung eines Punktes auf der Achse bleibt der Nullpunkt der Punkt der 1/4-Ebene, der dem bewegten Punkt am nächsten ist.
D.h. die Achse ist ein Ort von Punkten des R4, die näher am Nullpunkt sind als an allen anderen Punkten der 1/4-Ebene. Wie also kann sich ein Punkt vom Nullpunkt wegbewegen, ohne einem anderen Punkt der 1/4-Ebene nahezukommen ? Zwei verschiedene Möglichkeiten: Richtung x2 und x3.
Vermutlich gibt es einen einfach zu beweisenden Hilfssatz "ein n-dim Körper braucht eine n-2 dim Achse um zu rotieren ohne zu eiern." (A2: n-3dim-Achse genügt bei komplexem Rotationswinkel).

Die Punkte auf der Achse müssten unverändert bleiben bei der Rotation. Der komplexe Winkel besteht vermutlich aus einem normalen Winkel und einem Winkel in der Ebene mit der imaginären Achse, entsprechend einem normalen Winkel plus Lage im Raum.

Ob dann

muss man an der Reihenentwicklung prüfen und so die Definition recherchieren (Funktionentheorie). Gemeint vermutlich Recos(z)>1 oder |cos(z)|>1.
...

Was bedeutet nun Drehung und wie sieht das im R4 aus, bzw. im "euklidischen 4D-Raum mit 1 imaginären Koordinate" (obwohl Euklid schon lange tot war).
Def. Eukl.Raum: ...
...

Bild: Euklidischer 4D-Raum mit 4 aufeinander senkrecht stehenden Koordinatenachsen.
Die blauen Punkte sind näher am Nullpunkt als an jedem anderen Punkt des 3D-Raumes x1,2,3.

______________________________________________________________________________
allgemein:

Vielleicht kann man es sich so vorstellen, dass sich die Lichtgeschwindigkeit nicht zu mechanischen Geschwindigkeiten addiert: Das Licht geht sozusagen von einem eingefrorenen Momentanzustand der Materie aus. Wie das aus versch. Bezugssystemen heraus aussieht, muss ich mir noch überlegen, und ob diese Betrachtungsweise etwas bringt. (Massenzunahme und alle anderen Beobachtungen müssen erklärt werden)

Bei den Berechnungen der versch. Bezugssysteme wird der Nullpunkt so verschoben, dass alle Nullpunkte der versch.Systeme zusammenfallen. Der Beobachter sitzt also nicht im Nullpunkt des Koordinatensystems. Wenn man davon ausgeht, dass alle Nullpunkte des Universums in einem (beliebigen) Punkt zusammenfallen, hilft das vielleicht bei einer Vorstellung des Gesamtsystems.

Lässt sich die Gleichwertigkeit der Bezugssysteme vielleicht damit erklären, dass alle Beobachter gleich weit entfernt sind vom Mittelpunkt des Universums. (=Mittelpunkt der 4D-Kugel von der das Universum die Oberfläche sein soll, oder 5D). Dagegen spricht die enorme Flachheit des Raums, wie ich gehört habe. Die Messung der Raumkrümmung könnte evtl. durch noch kompliziertere Strukturen verhindert werden, z.B. Dreieck aus Lichtstrahlen (oder wie will man die Flachheit festgestellt haben?) hat Winkelsumme 180Grad obwohl Raumkrümmung vorhanden. (Das müsste dann eine andere Art von Raumkrümmung sein als die gravitative.)

Langsam komme ich in die richtige Stimmung, mir einen Schreibtisch einzurichten, sobald ich es mir leisten kann. Mit noch mehr Geld, und falls es mir jemand erklärt, könnte ich vielleicht die 50 Jahre in 3Jahren aufholen. In diesem Zusammenhang möchte ich nochmal auf die sorgfältigen Spaltungstendenzen innerhalb der CIA u.ä. hinweisen. Diese Seite soll helfen, dass sich Eingeborene vorbereiten, um die Aussagen von evtl. Überläufern überhaupt umsetzen zu können.
______________________________________________________________________________